Disjoint Sparse Table
Nguồn
![]() [Tutorial] Disjoint Sparse Table
[Tutorial] Disjoint Sparse Table
Giới thiệu
Trước khi đi vào cấu trúc của cấu trúc dữ liệu này, chúng ta hãy xem nó có thể làm được gì.
Cho một dãy \(A\) có độ dài \(N\) và \(Q\) truy vấn. Mỗi truy vấn yêu cầu bạn thực hiện một hàm \(F\) trên đoạn con \([L, R]\), nghĩa là \(F(A_L, A_{L+1}, \ldots, A_R)\).
Với sparse table bình thường, bạn có thể trả lời các truy vấn trong \(O(\log N)\) với \(\Theta(N \log N)\) tiền xử lý.
Gọi \(N' = 2 ^ {\lceil\log N\rceil}\), với Disjoint Sparse Table ta có thể trả lời các truy vấn trong \(\Theta(1)\) với \(\Theta(N' \log N')\) tiền xử lý.
Lưu ý:
- \(\log\) là theo hệ cơ số 2, hay còn gọi là logarit nhị phân
- Mảng \(A\) không thay đổi
- Hàm \(F\) là có tính chất kết hợp
- Nếu \(F\) là hàm idempotent, sparse table bình thường có thể trả lời truy vấn trong \(\Theta(1)\)
Thực sự thì bạn không nhất thiết phải dùng cấu trúc dữ liệu này trong hầu hết các bài toán, vì các bài với dữ liệu không đổi và time limit chật rất hiếm.
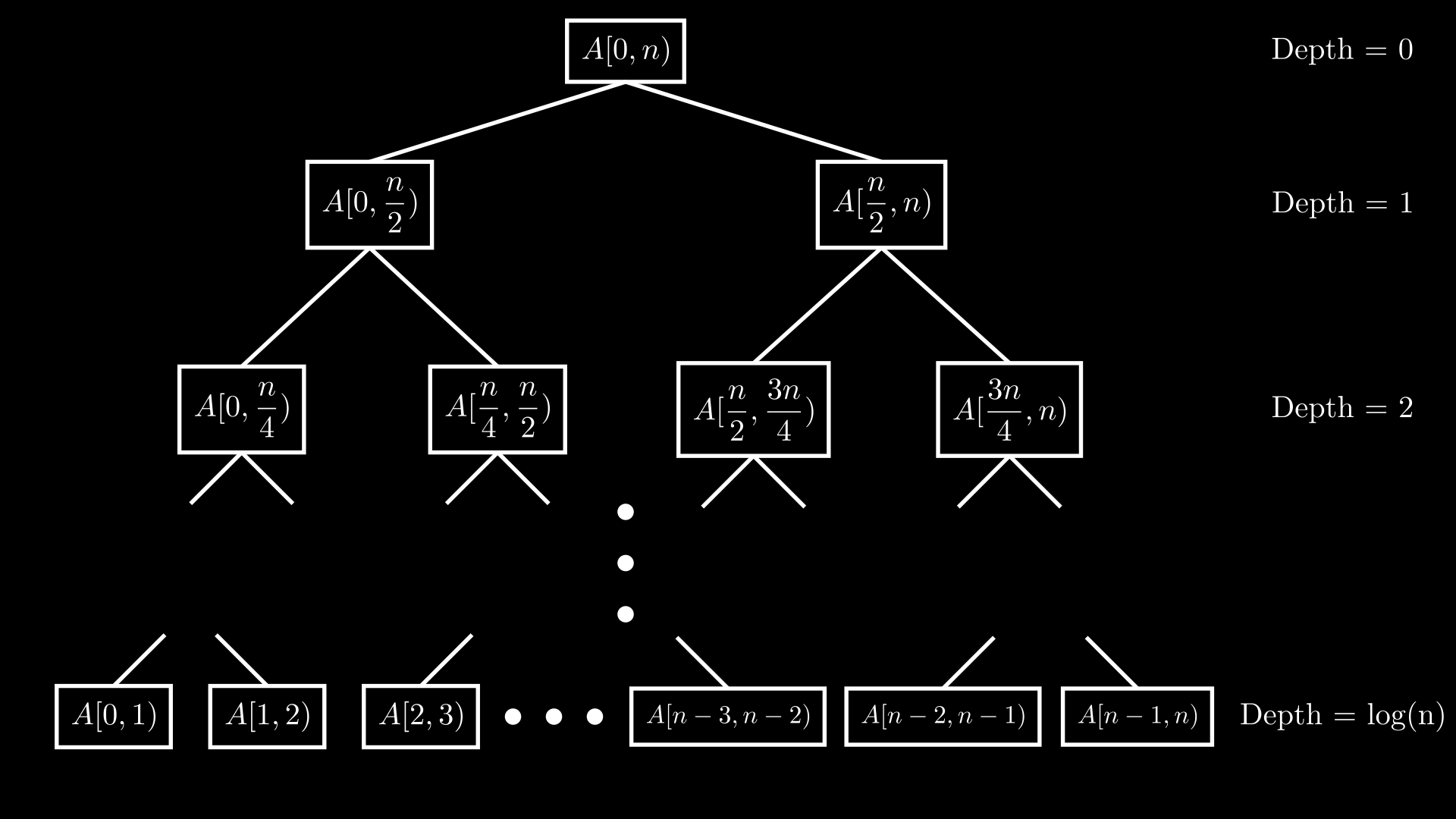
Cấu trúc
Cấu trúc của nó giống hệt segment tree. Mỗi node lưu thông tin liên quan đến đoạn mà nó quản lý \([L, R)\).
Xét một node quản lý đoạn \([L, R)\) và chỉ số ở giữa \(M = \frac{L + R}{2}\).
Node này lưu các giá trị tiền xử lý của
Nên kích thước node sẽ là \(R - L\). Nếu kích thước \(> 1\), nó sẽ có 2 node con tương ứng với các đoạn \([L, M)\) và \([M, R)\).
Cách xây dựng
Giờ để tạo node tương ứng với đoạn \([L, R)\), đầu tiên ta cần tính tất cả các giá trị tiền xử lý trong \(\Theta(R-L)\) và tạo các node con của nó.
Gọi độ phức tạp thời gian để xây dựng cây với node gốc có kích thước là \(X\) là \(T(X)\) thì ta có
Vậy thời gian để xây dựng cây DST là \(\Theta(N \log N)\).
Truy vấn
Ta có thể trả lời các truy vấn một cách đệ quy tương tự như khi làm với segment tree. Xét trường hợp ta đang ở node \([L, R)\) và ta cần trả lời truy vấn ứng với đoạn \([X, Y]\), thì
Nếu \(X \leq M \leq Y\), ta có thê trả lời trong \(\Theta(1)\) vì ta có thể chập kết quả của \([X, M]\) và \([M+1, Y]\) trong \(\Theta(1)\). Ngược lại nếu đoạn \([X, Y]\) nằm hoàn toàn trong một node con nào đó, ta di chuyển xuống node đó để thực hiện truy vấn.
Vậy độ phức tạp thời gian của việc truy vấn sẽ là \(O(\log N)\). Lưu ý là trường hợp xấu nhất xảy ra có thể ví dụ như khi \(X = Y = \frac{N}{2} - 1\).
Cải thiện độ phức tạp
Giờ ta hãy tăng kích thước mảng \(A\) lên thành \(N' = 2 ^ {\lceil\log N\rceil}\), nghĩa là kích thước mảng bây giờ là một luỹ thừa của \(2\). Lưu ý là điều này không làm thay đổi kết quả của bất kỳ truy vấn nào. Gọi \(x = \lceil\log N\rceil\).
Xét node thứ \(j\) (đánh số từ 0, từ trái sang) ở độ sâu \(i\). Kích thước của nó là \(\frac{N'}{2 ^ i}\). Nó sẽ tương ứng với đoạn \([\frac{N'}{2 ^ i} \times j, \frac{N'}{2 ^ i} \times (j + 1))\), \(M = j \times \frac{N'}{2 ^ i} + \frac{N'}{2 ^ {i + 1}}\)
Xét biểu diễn nhị phân của \(M\). Nó trông sẽ như sau:
Giả sử ta được yêu cầu trả lời truy vấn \([L, R]\). Ở đây ta bỏ qua trường hợp cơ bản là \(L = R\) và chỉ xét khi \(L < R\) thì biểu diễn nhị phân của \(L\) và \(R\) sẽ như sau:
Lưu ý là \(k_2 = \text{độ dài biểu diễn nhị phân} - \text{số số 0 phía trước của } L \oplus R - 1\)
Dễ thấy là \(L < M \leq R\). Hơn nữa có thể thấy rằng node ở độ sâu \(x - k_2 - 1\) nhận \(M\) là phần tử nằm giữa. Giờ ta cần xác nhận \([L, R]\) nằm hoàn toàn trong \([X, Y]\).
Biểu diễn nhị phân của \(X\) và \(Y\) như sau:
Suy ra \(X \leq L < R \leq Y\).
Vi xử lý máy tính chúng ta có thao tác BSR (Bit Scan Reverse) nên ta có thể xác định được node quản lý đoạn \([X, Y]\) trong \(\Theta(1)\).
Vậy nên giờ mỗi truy vấn có thể được trả lời trong \(\Theta(1)\)
Cài đặt
Ta thấy trên mỗi độ sâu thì tổng kích thước của các node bằng \(N\), vì vậy ta có thể dùng một mảng 2 chiều để lưu DST. Ví dụ với một bài toán như sau:
Truy vấn tích của đoạn
Cho một mảng \(A\) và một số \(P\), ta cần trả lời \(Q\) truy vấn có dạng: cho \(L\) và \(R\), \(0 \leq L \leq R < N\), tìm \(\prod_{i=L}^{R} A[i]\text{ (mod P)}\).
Ta cài đặt như sau:
struct DisjointSparseTable {
vi a;
int size, x;
ll p;
vector<vi> table;
DisjointSparseTable(vi &a, int p) {
// tất cả chỉ số bắt đầu từ 0
// đầu vào là mảng A và số P
this->a = a;
this->p = p;
// x =floor(log_2(n))
// size = 2^x = 2^floor(log_2(n))
size = SZ(a);
x = __builtin_clz(SZ(a)) ^ 31;
if( (1<<x) != SZ(a)) size = (1<<(++x));
// cập nhật độ dài mảng A
this->a.resize(size);
// tạo sparse table, có x+1 level (từ 0 đến x như hình trên)
// mỗi level có kích thước là size
table.resize(x+1, vi(size));
// fill vào table này
build();
}
void build() {
int len = 1;
// fill bảng từ level quản lý node lá lên
FORE(level,x,0) {
for (int l = 0; l < size; l += len) {
// lưu ý đoạn này là [l, r), không phải [l, r]
int r = l + len;
// mid ở đây sẽ có dạng xxxxx01111
// tương tự mid + 1 sẽ là xxxxx10000
int mid = (l + r) >> 1;
// bắt đầu fill vào 2 đoạn từ mid và mid+1, theo 2 hướng khác nhau
table[level][mid] = a[mid] % p;
FORE(i,mid-1,l) table[level][i] = (ll) table[level][i+1] * a[i] % p;
if (mid + 1 < r) {
table[level][mid+1] = a[mid+1] % p;
FOR(i,mid+2,r-1) table[level][i] = (ll) table[level][i-1] * a[i] % p;
}
}
len <<= 1;
}
}
int query(int l, int r) {
// truy vấn trên đoạn [l, r]
if (l == r) {
// trường hợp cơ bản
return a[l] % p;
}
// lấy độ dài k2 như trong phần chứng minh
int k2 = __builtin_clz(l ^ r) ^ 31;
// lấy level của đoạn
int lev = x - 1 - k2;
// tính kết quả đoạn bên trái
int ans = table[lev][l];
if (r & ((1<<k2) - 1)) {
// nếu y % (1<<k2), nghĩa là có đoạn bên phải, ta thêm đoạn bên phải vào
ans = (ll) ans * table[lev][r] % p;
}
return ans;
}
};
Luyện tập
| Problem | Status | Submission | Code | Date |
|---|---|---|---|---|
| Codechef - SEGPROD |  |
Submission | Code | 29/11/2022 |