Cây DFS và ứng dụng
Nguồn
![]() [Tutorial] The DFS tree and its applications: how I found out I really didn't understand bridges
[Tutorial] The DFS tree and its applications: how I found out I really didn't understand bridges
Cây DFS
Cho một đồ thị \(G\) vô hướng liên thông. Chạy DFS trên đồ thị đó với điểm gốc bất kỳ, có thể cài đặt như sau:
function visit(u):
mark u as visited
for each vertex v among the neighbors of u:
if v is not visited:
mark the edge uv
call visit(v)
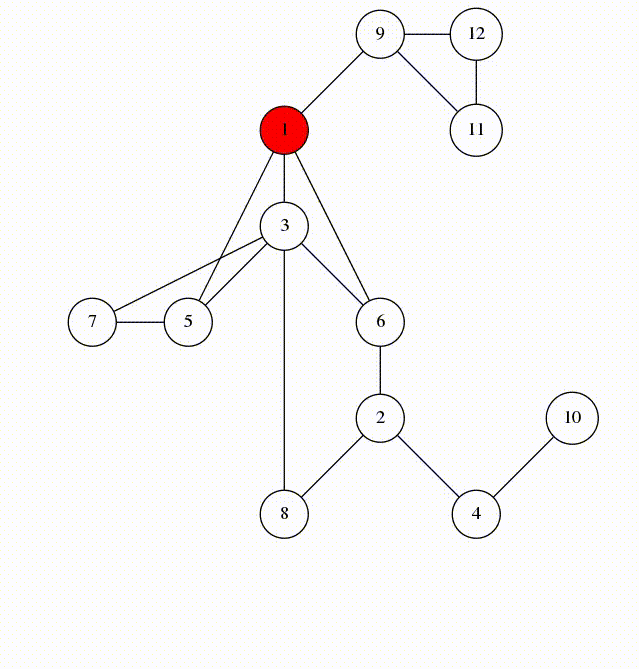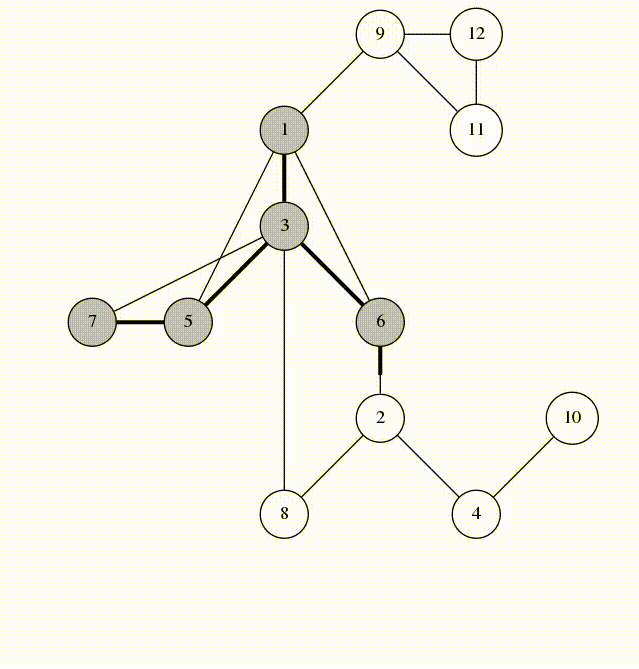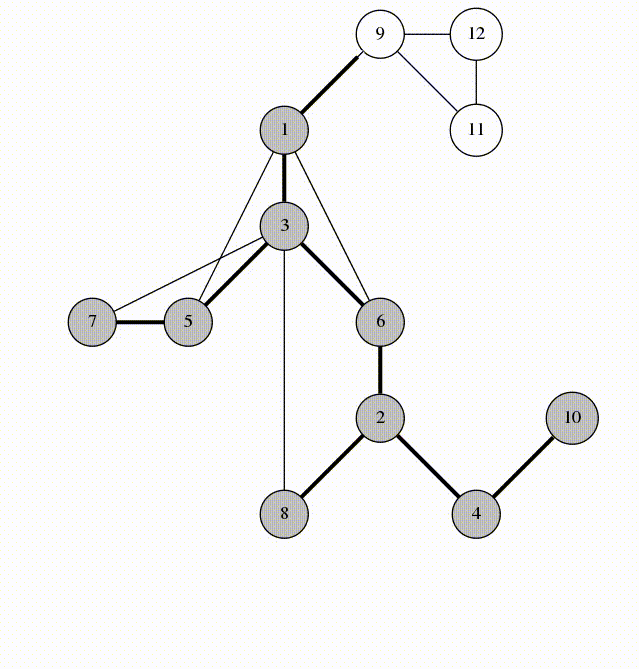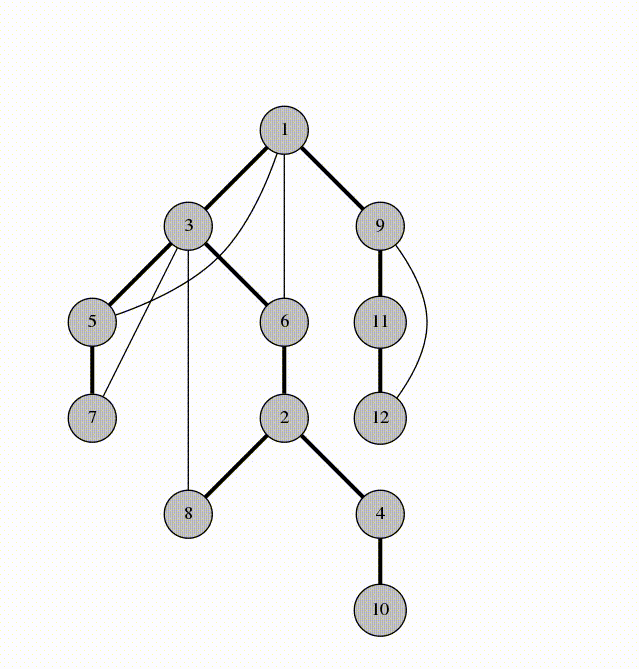
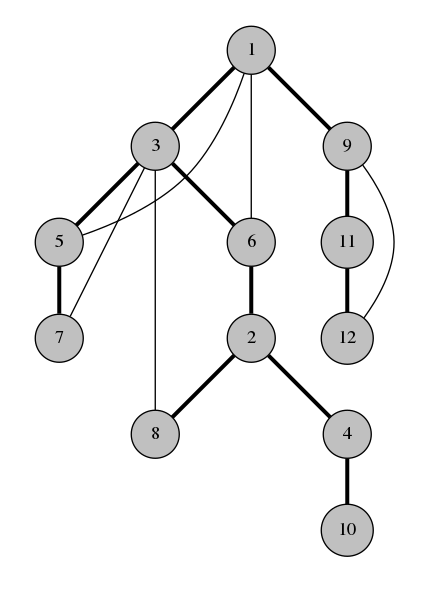
Nếu ta visit(1) thì nó sẽ như thế này:
Nhìn vào các cạnh được đánh dấu trên dòng số 5. Chúng tạo thành một cây khung của \(G\) với gốc là 1. Chúng ta gọi những cạnh này là cạnh xuôi (span-edges). Các cạnh còn lại là các cạnh ngược (back-edges). Cây DFS cuối cùng sẽ như sau:
Observation 1
Các cạnh ngược trên đồ thị kết nối 1 node với con cháu của nó trên cây khung. Đó là lý do vì sao cây DFS rất hữu dụng.
Vì sao?
Giả sử có cạnh \(uv\), không mất đi tính tổng quát, ta giả sử \(u\) được thăm trước \(v\) (lúc này \(v\) chưa được thăm). Ta có:
-
Nếu DFS đi đến \(v\) từ \(u\) dùng cạnh \(uv\), \(uv\) là cạnh xuôi
-
Nếu DFS không đi đến \(v\) từ \(u\) dùng cạnh \(uv\), thì \(v\) đã được thăm ở trước đó ở line số 4 trong mã giả. Vì vậy nó đã được thăm trên 1 đỉnh con của \(u\), nên \(v\) là con cháu của \(u\) trên cây DFS.
Trở lại với ví dụ trên, đỉnh 4 và 8 không có cạnh ngược kết nối chúng vì đỉnh này không phải tổ tiên của đỉnh kia và ngược lại. Nếu có cạnh nối 4 và 8, DFS sẽ đi đến 8 từ 4 thay vì về 2.
Đây là Observation quan trọng nhất về cây DFS. Cây DFS rất mạnh vì nó đơn giản hoá đồ thị. Thay vì phải quan tâm đến quá nhiều loại cạnh, ta chỉ cần biết đến 1 cái cây và vài cạnh nối cha-con đơn thuần. Điều này làm nó dễ cài đặt và suy nghĩ.
Tìm cầu
Cây DFS và Observation 1 ở trên là cốt lõi của thuật tìm cầu Tarjan. Một số hướng dẫn tìm cầu trên mạng chỉ nói về cây DFS sương sương và định nghĩa những thứ mơ hồ như \(dfs[u]\) và \(low[u]\). Quên hết chúng đi. Đó không phải cách dễ hiểu để tìm cầu, \(dfs[u]\) chỉ là 1 cách lộn xộn để kiểm tra xem 1 node có phải cha của 1 node khác hay không. Trong khi đó, \(low[u]\) thì còn khó giải thích hơn nữa.
Giờ chúng ta sẽ tìm cầu trên 1 đồ thị vô hướng liên thông \(G\). Xét cây DFS của \(G\).
Observation 2
Một cạnh xuôi \(uv\) là cầu khi và chỉ khi không tồn tại cạnh ngược kết nối con cháu của \(uv\) với tổ tiên của \(uv\). Nói cách khác, cạnh xuôi \(uv\) là cầu khi và chỉ khi không có cạnh ngược "chạy qua" \(uv\).
Vì sao?
Xóa cạnh \(uv\) chia cây khung ra thành 2 phần tách nhau: cây con gốc \(uv\) và phần còn lại. Nếu có cạnh ngược nối 2 phần này, đồ thị vẫn được kết nối, ngược lại \(uv\) là cầu. Cách duy nhất 1 cạnh ngược có thể kết nối 2 phần này là khi nó kết nối con cháu của \(uv\) với tổ tiên của \(uv\).
Ví dụ, xét cây ở hình trên, cạnh 6-2 không phải cầu, vì khi xóa nó, cạnh ngược 3-8 vẫn kết nối 2 phần. Ngược lại, cạnh 2-4 là cầu vì không có cạnh ngược nào tương tự.
Observation 3
Cạnh ngược chắc chắn không phải cầu
Điều này dẫn về thuật tìm cầu cơ bản. Cho đồ thị \(G\):
- Tìm cây DFS của nó.
- Với mỗi cạnh xuôi \(uv\), nếu có không có cạnh ngược “chạy qua” \(uv\), nó là cầu.
Vì cấu trúc đơn giản của cây DFS, step 2 rất dễ cài. Ví dụ, bạn có thể dùng cách \(low[u]\). Hoặc bạn có thể dùng prefix sum. Gọi \(dp[u]\) là số cạnh ngược “chạy qua” cạnh nối \(u\) và \(parent[u]\). Khi đó,
Cạnh xuôi nối u và \(parent[u]\) là cầu khi và chỉ khi \(dp[u] = 0\)
Chọn hướng cạnh để tạo đồ thị liên thông mạnh
Cho bài tập như sau, từ 118E - Bertown Roads.
Problem 1
Cho đồ thị vô hướng liên thông \(G\). Chỉ hướng cho từng cạnh để tạo thành đồ thị liên thông mạnh hoặc trả về impossible.
Observation 4
Nếu \(G\) có cầu, trả về impossible.
Vì sao?
Đơn giản vì nếu \(uv\) là cầu và ta chọn hướng \(u \to v\), sẽ không có đường đi từ \(v\) đến \(u\)
Giả sử đồ thị không có cầu, xét cây DFS của nó. Chỉ hướng cạnh xuôi hướng xuống và cạnh ngược hướng lên, ta có:
Observation 5
Có đường đi từ gốc đến tất cả các node khác.
Vì sao?
Đơn giản vì bạn có thể đi xuống nhờ cạnh xuôi.
Observation 6
Có đường đi từ tất cả về gốc
Vì sao?
Xét 1 node \(v\) không phải gốc. Gọi \(u\) là cha của nó trên cây khung. Vì đồ thị không có cầu, sẽ phải có 1 cạnh ngược “chạy qua” \(uv\): nó kết nối con cháu của \(v\) và tổ tiên của \(u\). Ta có thể đi xuống từ \(v\) tới cạnh ngược đó, sau đó dùng nó để về đến tổ tiên của \(u\). Dùng cách này ta đến gần node gốc hơn. Lặp lại đến khi về gốc.
Vì vậy, đồ thị liên thông.
Cài đặt cacti (rừng xương rồng)
Đôi khi cây DFS chỉ là 1 cách để biểu diễn đồ thị theo kiểu làm cho nó dễ cài đặt hơn, giống danh sách kề nhưng ở đẳng cấp cao hơn. Phần này đơn thuần chỉ là 1 trick cài đặt.
1 cactus (cây xương rồng) là 1 đồ thị mà mỗi cạnh (hoặc đôi khi, đỉnh) thuộc về nhiều nhất 1 chu trình đơn. Trường hợp đầu gọi là cạnh xương rồng, trường hợp sau gọi là đỉnh xương rồng. Rừng xương rồng có cấu trúc đơn giản hơn đồ thị thông thường, nên người ta có thể giải bài trên nó dễ hơn trên đồ thị truyền thống. Nhưng dễ hơn ở trên giấy thôi: các thuật xương rồng khi cài thường rất khó chịu nếu bạn không biết mình đang làm gì.
Trên cây DFS của xương rồng, với mỗi cạnh xuôi, có nhiều nhất 1 cạnh ngược “chạy qua” nó. Như vậy các chu trình trong cây này tương tự như 1 chu trình đơn: Mỗi cạnh ngược tạo 1 chu trình đơn với các cạnh xuôi nó “chạy qua”. Không có chu trình đơn nào khác.
Đó gần như là tất cả các tính chất của cây xương rồng.
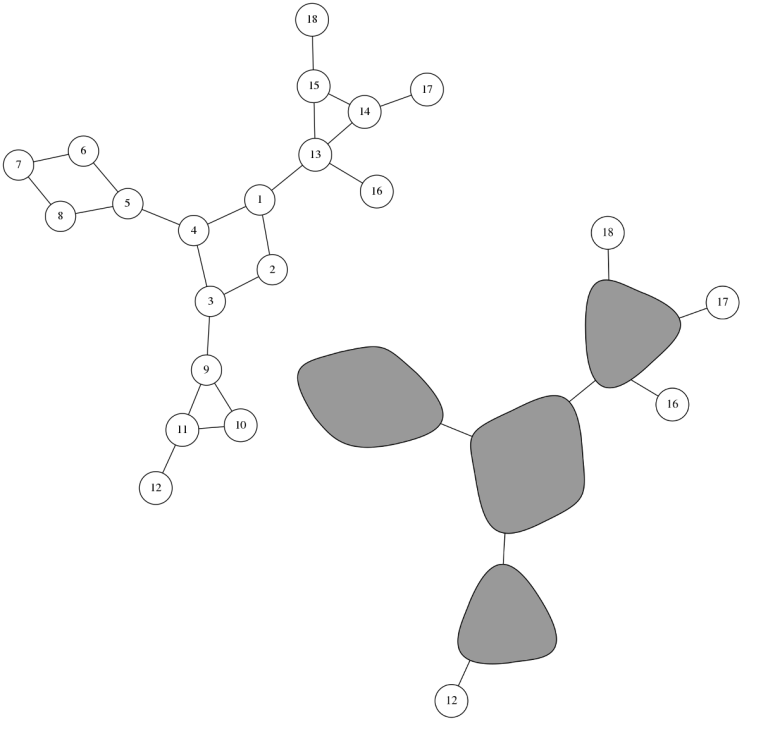
Ví dụ, xét đề bài sau:
Problem 2
Cho 1 đồ thị xương rồng liên thông \(N\) đỉnh. Trả lời các truy vấn có dạng: Có bao nhiêu đường đi đơn khác nhau từ \(p\) đến \(q\)?
Đây là bài 231E - Cactus. Lời giải chính thức nhìn như thế này:
- Bóp mỗi chu trình thành 1 đỉnh, tô đỉnh này màu đen
- Như vậy đồ thị sẽ thành 1 cây, chọn gốc của cây
- Với mỗi đỉnh \(u\), đếm số đỉnh đen trên đường đi từ gốc đến \(u\), gọi nó là \(cnt[u]\)
- Đáp án của query \((p, q)\) sẽ là \(2 ^ {cnt[p] + cnt[q] - 2 * cnt[lca(p, q)]}\) hoặc \(2 ^ {cnt[p] + cnt[q] - 2 * cnt[lca(p, q)] + 1}\) tuỳ vào màu của \(lca(p, q)\)
Không khó để hiểu lời giải này, nhưng điều thú vị lại nằm ở cách cài step 1.
Sau 1 hồi suy nghĩ, bạn có thể tìm được cách cài cho step 1 ở trên, nhưng có 1 cách dễ hơn dùng cây DFS:
- Gán cho mỗi cạnh ngược 1 index bắt đầu từ \(N + 1\)
- Với mỗi đỉnh \(u\), tìm index của cạnh ngược chứa \(u\) (đi lên), gọi đó là \(cycleId[u]\), nếu \(u\) không nằm trong chu trình thì \(cycleId[u] = u\)
- Tạo một danh sách kề mới mà với mỗi \(u\), mỗi instance của \(u\) sẽ được thay bằng \(cycleId[u]\)
Step 2 sẽ trông như thế này:
function visit(u):
for each vertex v among the children of u:
visit(v)
if there is a back-edge going up from u:
cycleId[u] = the index of that back-edge
else:
cycleId[u] = u
for each vertex v among the children of u:
if cycleId[v] != v and there is no back-edge going down from v:
cycleId[u] = cycleId[v]
Xóa cạnh để tạo đồ thị hai phía
Problem 3
Xét một đồ thị vô hướng. Tìm số cách xoá 1 cạnh để tạo ra đồ thị hai phía.
Đây là bài 19E - Fairy. Bài này không có lời giải chính thức, nhưng lời giải không chính thức dùng cấu trúc dữ liệu phức tạp như là Link cut tree. Chúng ta sẽ giải quyết nó bằng cây DFS.
Trong đề bài, đồ thị không nhất thiết phải liên thông. Tuy nhiên, ta thấy:
- Nếu đồ thị gồm toàn thành phần liên thông 2 phía, xóa bất kỳ cạnh nào cũng tạo thành đồ thị 2 phía.
- Nếu đồ thị gồm nhiều thành phần liên thông không phải 2 phía, thì ta không thể tạo đồ thị 2 phía bằng cách xoá 1 cạnh.
Vì vậy, trường hợp ta cần xét ở đây là trường hợp có 1 thành phần liên thông không phải 2 phía. Rõ ràng cạnh cần xoá là cạnh từ thành phần liên thông đó, ta có thể giả sử rằng nó là thành phần liên thông duy nhất trong đồ thị. Từ giờ, ta giả sử rằng ta có 1 đồ thị liên thông, không phải 2 phía.
Xét cây DFS của đồ thị này. Ta tô màu cây này sao cho cạnh xuôi nối node đen và node trắng. Một số cạnh ngược có thể kết nối 2 node cùng màu. Gọi các cạnh này là các cạnh “mâu thuẫn", ngược lại, cạnh ngược nối 2 node khác màu gọi là “không mâu thuẫn”.
Observation 7
Một cạnh ngược \(uv\) là đáp án khi và chỉ khi \(uv\) là cạnh mâu thuẫn duy nhất
Vì sao?
Nếu ta xoá cạnh ngược mâu thuẫn duy nhất trong đồ thị, đồ thị bây giờ được tô 2 màu, nên nó là đồ thị 2 phía
Nếu đồ thị có những cạnh mâu thuẫn khác hoặc ta xoá cạnh ngược không mâu thuẫn, những cạnh mâu thuẫn còn lại tiếp tục tạo ra chu trình lẻ và đồ thị sẽ không thể là đồ thị 2 phía.
Observation 8
Một cạnh xuôi \(uv\) là đáp án khi và chỉ khi các cạnh ngược “chạy qua” nó đều là cạnh mâu thuẫn.
Vì sao?
Nếu ta xoá cạnh xuôi \(uv\), cây khung sẽ bị chia làm 2 phần: cây con của \(uv\) và phần còn lại. Các cạnh xuôi khác vẫn sẽ phải nối node đen và node trắng. Vì vậy cách duy nhất để tô màu đồ thị là đảo ngược màu cho cây con \(uv\).
Cạnh xuôi \(uv\) sẽ là đáp án khi và chỉ khi đảo màu làm tiêu biến hết các cạnh mâu thuẫn và không tạo ra cạnh mâu thuẫn mới. Điều này xảy ra khi và chỉ khi các cạnh mâu thuẫn này nối cây con \(uv\) với phần còn lại của đồ thị.
Vậy ta giải bài như sau:
- Tìm cây DFS của đồ thị và tô màu cho nó.
- Nếu chỉ có 1 cạnh ngược mâu thuẫn, thêm nó vào đáp án.
- Dùng DP để tính, với mỗi cạnh xuôi, có bao nhiêu cạnh ngược mâu thuẫn và không mâu thuẫn “chạy qua” nó.
- Nếu 1 cạnh xuôi gồm toàn cạnh mâu thuẫn chạy qua, thêm nó vào đáp án.
Với đồ thị có hướng
Nếu ta duyệt cây DFS của đồ thị có hướng thì sao:
function visit(u):
mark u as visited
for each vertex v among the neighbors of u:
if v is not visited:
mark the edge u->v
call visit(v)
Sẽ có một số trường hợp duyệt không đến được một số node. Để đơn giản thì giả sử rằng:
- Ta bắt đầu từ node 1
- Có thể thăm tất cả các đỉnh từ đỉnh 1
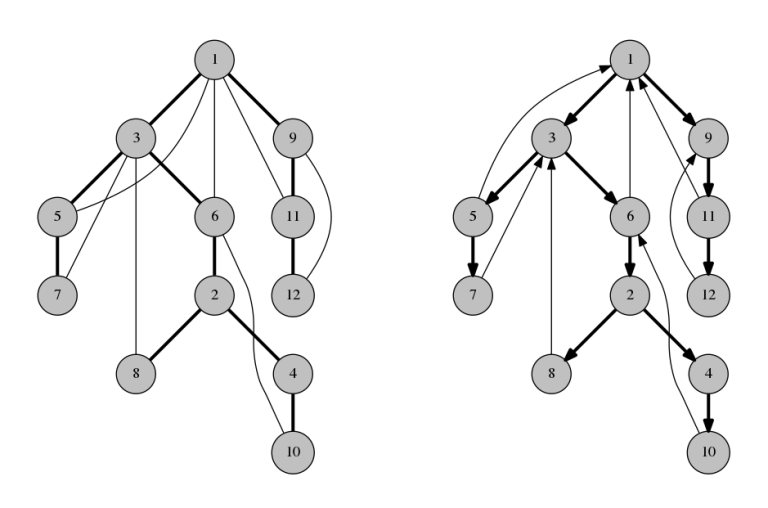
Gọi các cung được đánh dấu ở dòng 5 là cung xuôi
Observation 9
Các cung xuôi tạo một cây khung có gốc, có hướng xa ra khỏi node gốc.
Các cung khác sẽ rơi vào các trường hợp sau:
- Cung nối con cháu và tổ tiên: cung ngược
- Cung không như vậy: cung chéo
Có thể chia các cung ngược thành cung lên hoặc cung xuống tuỳ vào hướng của chúng.
Observation 10
Các cung chéo luôn hướng từ đỉnh thăm sau về đỉnh thăm trước
Vì sao?
Giả sử có cung \(u \to v\), và DFS đến \(u\) nhưng chưa đến \(v\). Ta có:
- Nếu DFS không đi từ \(u\) đến \(v\), nghĩa là phép duyệt đã thăm \(v\) khi thăm một con khác của \(u\) rồi nên \(u \to v\) là cung ngược
- Nếu phép duyệt đi từ \(u\) đến \(v\), cung \(u \to v\) là cung xuôi
Vì vậy \(u \to v\) là cung chéo khi phép duyệt đến \(v\) trước \(u\)
Biến thể có hướng của cây DFS được dùng để tạo dominator tree của đồ thị có hướng, nhưng đó lại nằm ngoài phạm vi bài viết này và xứng đáng có 1 bài riêng.
Nhận xét về phương pháp DP
Lưu ý: Phần này không có trong bài gốc của tác giả mà là cảm nhận của cá nhân mình khi luyện tập các bài trong chủ đề này.
Ưu điểm
Thứ nhất, phương pháp này khá dễ hiểu với mình. Mình thấy nó giúp giải quyết phần lớn các bài trong 8 bài đầu tiên của phần luyện tập một cách cực kỳ dễ dàng (Các bài chọn hướng cho cạnh).
Thứ hai, các Observation trong bài viết cùng với các phần chứng minh rõ ràng đã giúp mình rất nhiều trong việc hiểu được tính chất của cây DFS. Mình thấy nó giải đáp rất tốt các thắc mắc mà các bạn có thể có trong cuốn Giải thuật và Lập trình của thầy Lê Minh Hoàng (sách này trình bày cách dùng \(num[u]\) và \(low[u]\), lần đầu mình đọc nó thấy khá là rắc rối)
Nhược điểm
Tuy nhiên, phương pháp này tồn tại một nhược điểm rất lớn. Đó chính là sự khó khăn trong việc tìm khớp (articulation point) của đồ thị. Khi mình đọc bình luận của bài viết gốc trên Codeforces, mình không thực sự thấy ai có thể tìm được khớp của đồ thị bằng cách này mà hầu như toàn đoán hoặc trả lời sai (ngay chính tác giả cũng có trả lời sai). Vì sao nó lại khó khăn đến như vậy?
Xét một đỉnh \(u\) trên cây DFS. Để \(u\) là một khớp của đồ thị, ta cần có những điều kiện sau đây:
- Giả sử \(u\) không phải gốc của cây DFS. \(u\) là khớp của đồ thị khi và chỉ khi tồn tại một nhánh con của \(u\) (gọi là \(v\)) không có cạnh ngược "đi qua" cạnh nối giữa \(u\) và cha của \(u\). Như vậy là với mỗi đỉnh con \(v\) thì bạn phải kiểm tra xem các cạnh ngược trong \(dp[v]\) có vượt qua đỉnh \(u\) hay không. Nếu tất cả đều không qua thì \(u\) mới là khớp. Nghĩ thôi đã thấy làm kiểu này rất mệt não khi bạn cần thông tin của \(u\) với mỗi \(v\) trong khi bạn chỉ có thông tin to đùng của \(dp[u]\) và các \(dp[v]\).
- Khi \(u\) là gốc của cây DFS, \(u\) là khớp của đồ thị khi và chỉ khi nó có nhiều hơn 1 nhánh con. Trường hợp này thì dễ xử lý hơn nhiều.
Đến đây thì mình rẽ hướng sang việc tìm hiểu lại cách dùng \(num[u]\) và \(low[u]\) và mình thấy rất dễ hiểu. Chỉ với một điều kiện, bạn đã có thể giải quyết trường hợp khó nhằn ở trên. Mình khởi động phương pháp này với bài VN SPOJ - GRAPH_.
Đại khái thì \(num[u]\) là số thứ tự của đỉnh được thăm đầu tiên đến đỉnh thăm sau cùng, cứ đến đâu thì đánh số cho đỉnh đó theo thứ tự tăng dần của số. Còn \(low[u]\) là giá trị numbering nhỏ nhất trong các đỉnh có thể đến được từ một đỉnh \(v\) nào đó của nhánh DFS gốc \(u\) bằng một cung (với giả thiết rằng \(u\) có một cung giả nối với chính \(u\)). Định nghĩa phức tạp như vậy nhưng nếu bạn đã đọc bài viết này thì thấy nó cũng bình thường thôi.
Như vậy ban đầu khi thăm \(u\), ta đánh số thứ tự thăm cho đỉnh \(u\) và khởi gán
Sau đó xét tất cả các đỉnh \(v\) nối từ \(u\)
- Nếu \(v\) đã được thăm thì ta cực tiểu hoá \(low[u]\) như sau (lưu ý là nó là num nhỏ nhất trong các đỉnh có thể đến được từ một đỉnh \(v\) nào đó của nhánh DFS gốc \(u\) bằng một cung):
- Nếu \(v\) chưa được thăm thì ta thăm \(v\) sau đó cực tiểu hoá \(low[u]\) như sau (cùng lưu ý như trên):
Vậy nếu tồn tại một đỉnh \(v\) mà \(low[v] \ge num[u]\) (\(u\) là cha của \(v\) trong cây DFS) thì \(u\) là khớp (nếu \(u\) là gốc của cây DFS thì nó cần nhiều hơn 1 nhánh con để thành điều kiện đủ). Còn nếu \(low[v] > num[u]\) thì cạnh \(uv\) là cầu. Rất đơn giản.
Về bài COI 2006 - Policija
Cá nhân mình thấy bài này thực sự thách thức với người không quen làm các bài khớp cầu như thế này. Về cơ bản, đề bài cho một đơn đồ thị vô hướng. Ta có thêm \(Q\) truy vấn bao gồm 2 loại truy vấn.
- Truy vấn 1: cho 2 đỉnh \(u\) và \(v\), hỏi xem nếu ta cắt 1 cạnh \(xy\) trên đồ thị thì \(u\) và \(v\) có cùng thành phần liên thông hay không.
- Truy vấn 2: cho 2 đỉnh \(u\) và \(v\), hỏi xem nếu ta bỏ 1 đỉnh \(x\) trên đồ thị thì \(u\) và \(v\) có cùng thành phần liên thông hay không.
Dễ dàng thấy được là cạnh \(xy\) trong truy vấn 1 trước hết cần phải là cầu, còn đỉnh \(x\) trong truy vấn 2 trước hết cần phải là khớp. Trước khi đi vào giải quyết từng loại truy vấn, chúng ta cần giải quyết một vấn đề, cho 2 đỉnh \(u\) và \(v\), làm sao biết \(u\) có phải tổ tiên của \(v\) trên cây DFS hay không? Vì ta đã có một cái cây, ta có thể làm phẳng nó ra thành một mảng để một đỉnh sẽ phụ trách một đoạn trên mảng. Sau đó, \(u\) là tổ tiên của \(v\) khi đoạn của \(v\) nằm trọn trong đoạn của \(u\).
Truy vấn 1
Giả sử \(y\) là con của \(x\) trên cây DFS mà không làm mất đi tính tổng quát. Ta kiểm tra xem \(u\) và \(v\) có phải là con cháu của \(y\) trên cây DFS hay không. Nếu không đỉnh nào hoặc cả 2 đều thoả mãn, rõ ràng chúng cùng thành phần liên thông khi cắt cạnh \(xy\), ngược lại thì không cùng thành phần liên thông.
Truy vấn 2
Nếu không đỉnh nào là con cháu của \(x\) trên cây DFS, chúng rõ ràng cùng thành phần liên thông khi bỏ đỉnh \(x\)
Nếu có một đỉnh là con cháu của \(x\), ta xét xem nó có phải tác nhân làm cho \(x\) là khớp hay không, nếu có thì \(u\) và \(v\) không cùng thành phần liên thông (bởi vì nếu nó không phải tác nhân, bạn vẫn có thể đi lên đỉnh cha của \(x\) và từ đó đi tới đỉnh còn lại)
Nếu cả 2 đều là con cháu của \(x\), đầu tiên chúng cùng thành phần liên thông nếu chúng ở chung nhánh. Nếu khác nhánh, chúng không cùng thành phần liên thông khi một trong 2 ở nhánh tác nhân. Còn lại thì chúng cùng thành phần liên thông.
Tuy nhiên làm sao để kiểm tra nó có phải là tác nhân không. Như đã nói, nếu tồn tại một đỉnh \(v\) mà \(low[v] \ge num[u]\) (\(u\) là cha của \(v\) trong cây DFS) thì \(u\) là khớp. Làm sao để lấy được đỉnh con của \(x\) mà từ đó nó đi xuống được đỉnh con cháu đang xét? Ta dùng binary lifting để tìm tổ tiên thứ \(k\) của một đỉnh trên cây.
Kết luận
Tổng kết lại thì mình thấy bài này sử dụng khá nhiều kỹ thuật mà nếu bạn làm không quen, bạn sẽ mất rất nhiều thời gian suy nghĩ và đôi khi cách làm của bạn lại rất rất dài. Mong là qua đây các bạn sẽ thấy thú vị với phần nhận xét và bài tập này.
Luyện tập
Các bài cần tìm block-cut tree