Lấy mẫu hồ chứa (Reservoir Sampling)

Nguồn

LeetCode 382 - Linked List Random Node - Editorial

Mở đầu

Mình gặp một bài tập khá thú vị trên LeetCode mà mình nghĩ là ít người gặp khi thi Competitive Programming, có điều mình thấy nó khá hay. Đó là bài tập về lấy mẫu trong một list (mảng, linked list gì đó). Nghe có vẻ đơn giản nhưng với các giới hạn đi kèm, nó thực sự đáng để lưu lại.

Lấy mẫu hồ chứa (Reservoir Sampling) là một lớp của các thuật toán ngẫu nhiên để lấy mẫu trong một không gian mẫu không xác định được số lượng.

Đề bài

Cho một linked list đơn, trả về giá trị của một node ngẫu nhiên nào đó trên linked list này. Tuy nhiên, mỗi node phải có cùng xác suất được chọn.

Bạn cần cài class Solution như sau:

Solution(ListNode head): Khởi tạo object với một tham số là head của linked list.
int getRandom(): Chọn một node từ linked list và trả về giá trị của nó. Tất cả các node của linked list cần có tỉ lệ được chọn bằng nhau.

Follow up:

Giải như nào khi linked list cực lớn và độ dài bạn không biết được?
Giải như nào để không phải dùng thêm bộ nhớ?

Các cách tiếp cận

Cách tiếp cận 1: Lấy mẫu cố định

Nếu ta được cho một mảng hoặc linked list mà đã biết kích thước, ta có thể dễ dàng giải được bài này.

Nếu được cho một linked list, ta có thể chuyển nó thành một mảng. Với mảng, ta có thể biết được kích thước của nó và có thể truy cập vào từng phần tử ngay lập tức.

Ta được yêu cầu cài 2 hàm trong object, bao gồm hàm init(head) và getRandom().

Hàm init(head) sẽ được gọi khi khởi tạo object. Ta sẽ chuyển đổi linked list đã cho thành một mảng.

Hàm getRandom() sẽ chỉ đơn giản là lấy mẫu từ mảng ở trên.

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    vector<int> range;

    Solution(ListNode* head) {
        srand(time(NULL));
        while (head != NULL) {
            range.push_back(head->val);
            head = head->next;
        }
    }

    int getRandom() {
        int pick = rand() % range.size();
        return range[pick];
    }
};
/**
 * Your Solution object will be instantiated and called as such:
 * Solution* obj = new Solution(head);
 * int param_1 = obj->getRandom();
 */

Cách giải trên rất đơn giản và nhanh. Nhưng nó đi kèm với hai nhược điểm:

Nó cần thêm bộ nhớ để lưu trữ các phần tử cho việc lấy mẫu, nên không thoả mãn điều kiện trong follow up (một cách giải với độ phức tạp bộ nhớ là hằng số).
Nó không thể giải quyết trường hợp khi ta có một danh sách với các phần tử được thêm vào, nghĩa là ta không có đủ bộ nhớ để lưu tất cả các phần tử. Giả sử ta có một luồng số, ta muốn chọn ngẫu nhiêu một số ở bất cứ thời điểm nào. Với cách giải trên thì ta phải lưu tất cả các số trong bộ nhớ, nên không thể mở rộng được.

Ta sẽ giải quyết 2 nhược điểm này trong cách tiếp cận 2.

Độ phức tạp thời gian:

Với hàm init(head), độ phức tạp thời gian là \(O(N)\), với \(N\) là số phần tử trong linked list.
Với hàm getRandom(), độ phức tạp thời gian là \(O(1)\). Sinh số ngẫu nhiên tốn \(O(1)\) và truy cập vào phần tử của mảng cũng vậy.

Độ phức tạp bộ nhớ:

\(O(N)\), vì ta phải lưu thêm các phần tử của linked list vào một mảng.

Cách tiếp cận 2: Lấy mẫu hồ chứa

Để lấy mẫu ngẫu nhiên mà không biết kích thước mẫu với độ phức tạp bộ nhớ hằng số, ta dùng Lấy mẫu hồ chứa. Nó có thể giải quyết được hai nhược điểm của cách tiếp cận 1.

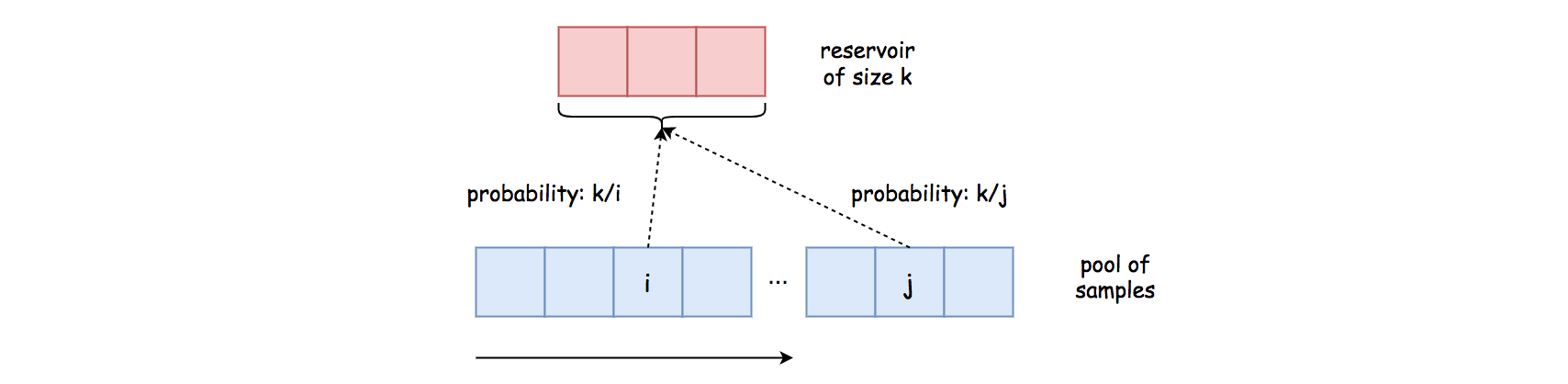
Thuật toán Lấy mẫu hồ chứa dùng để lấy mẫu \(k\) phần tử từ một quần thể có kích thước không xác định. Trong trường hợp này, \(k = 1\).

Lấy mẫu hồ chứa là một họ các thuật toán bao gồm nhiều biến thể qua thời gian. Ở đây ta sẽ nói về một thuật toán đơn giản, nhưng chậm, còn được gọi là Thuật toán R của Alan Waterman.

# S chứa các phần tử để lấy mẫu, R chứa kết quả lấy mẫu k phần tử
def ReservoirSample(S[1..n], R[1..k])
    # làm đầy hồ chứa trước đã
    for i := 1 to k
        R[i] := S[i]

    # thay thế các phần tử với xác suất giảm dần
    for i := k+1 to n
        # randomInteger(a, b) trả về một số nguyên trong đoạn [a, b]
        # các số có xác suất được chọn bằng nhau
        j := randomInteger(1, i)
        # nếu j nằm trong hồ chứa thì cho nó vào hồ chứa
        if j <= k
            R[j] := S[i]

Ta tóm tắt ý tưởng thuật toán như sau:

Đầu tiên, ta làm đầy hồ chứa \(R[]\) với các phần tử đầu tiên của mẫu \(S[]\). Đến cuối cùng, hồ chứa sẽ bao gồm các phần tử mà ta đã lấy từ mẫu.
Sau đó ta duyệt các phần tử còn lại của mẫu. Với mỗi phần tử, ta cần xác định xem ta có muốn cho nó vào hồ chứa hay không. Nếu có, ta thay thế phần tử trong hồ chứa với phần tử hiện tại.

Câu hỏi đặt ra ở đây là làm sao biết chắc rằng mỗi phần tử có xác suất được chọn bằng nhau?

Thuật toán trên đảm bảo rằng với mỗi phần tử đã được duyệt, chúng sẽ có xác suất được chọn vào hồ chứa bằng nhau.

Chứng minh như sau:

Giả sử ta có một phần tử ở vị trí \(i\) (và \(i > k\)), khi ta duyệt đến phần tử đó, xác suất được chọn vào hồ chứa của nó sẽ là \(\frac{k}{i}\), như ta thấy trong thuật toán.
Sau đó, có khả năng phần tử được chọn vào hồ chứa sẽ bị thay thế bởi một trong các phần tử sau nó. Cụ thể hơn, khi ta đến phần tử \(x\) (\(x > i\)), \(\frac{1}{x}\) sẽ là xác suất cho bất kỳ phần tử nào trong hồ chứa bị thay thế. Vì với bất kỳ vị trí nào trong hồ chứa, sẽ có \(\frac{1}{x}\) cơ hội nó sẽ bị chọn bởi hàm sinh số ngẫu nhiên. Ngược lại, xác suất sẽ là \(\frac{x-1}{x}\) cho bất cứ phần tử nào ở lại trong hồ chứa sau khi duyệt xong \(x\).
Tổng kết lại, để bất kỳ phần tử nào trong mẫu có thể được chọn vào hồ chứa kết quả, một dãy các biến cố độc lập sẽ phải xảy ra như sau:
- Thứ nhất, phần tử cần được chọn vào hồ chứa khi duyệt đến phần tử đó.
- Thứ hai, khi duyệt các phần tử tiếp theo, phần tử cần được chọn phải ở lại, nghĩa là không bị thay bởi các phần tử tiếp theo.
Như vậy, với một dãy số độ dài \(n\), xác suất để bất kỳ phần tử nào nằm trong hồ chứa kết quả sẽ theo công thức sau:

\[ \frac{k}{i} \cdot \frac{i}{i+1} \cdot \frac{i+1}{i+2} \dots \frac{n-1}{n} = \frac{k}{n} \]

Với phân tích trên, ta có thể cài như sau:

Trong hàm init(), ta chỉ cần lưu lại head của linked list, thay vì chuyển nó thành mảng.
Trong hàm getRandom(), ta lấy mẫu hồ chứa bắt đầu từ head của linked list. Cụ thể hơn là ta duyệt tất cả các phần tử lần lượt để xem thử ta có cần cho nó vào hồ chứa hay không (trong trường hợp này hồ chứa có \(1\) phần tử).

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode *head;

    Solution(ListNode* head) {
        this->head = head;
        // seed cho hàm sinh số ngẫu nhiên
        std::srand(std::time(0));
    }

    int getRandom() {
        // ở đây k = 1
        // chosenVal là kết quả
        // scope là số phần tử đã và đang duyệt qua
        int chosenVal = 0, scope = 1;
        ListNode *cur = head;
        while (cur != NULL) {
            // nếu random trúng phần tử đầu tiên thì thay thế nó
            // ở đây ta dùng chia lấy dư trong scope cho tiện
            if (std::rand() % scope == 0) {
                chosenVal = cur->val;
            }
            scope++;
            cur = cur->next;
        }
        return chosenVal;
    }
};

/**
 * Your Solution object will be instantiated and called as such:
 * Solution* obj = new Solution(head);
 * int param_1 = obj->getRandom();
 */

Độ phức tạp thời gian:

Với hàm init(head), độ phức tạp thời gian là \(O(1)\).
Với hàm getRandom(), độ phức tạp thời gian là \(O(N)\), với \(N\) là số phần tử trong linked list.

Độ phức tạp bộ nhớ:

\(O(1)\), vì các số các biến là hằng số, không tính linked list ban đầu.

Luyện tập

Problem	Submission	Code	Date
LC 382 - Linked List Random Node	Unavailable public link	Code	17/03/2023
LC 398 - Random Pick Index	Unavailable public link	Code	17/03/2023
LC 519 - Random Flip Matrix	Unavailable public link	Code	17/03/2023
LC 497 - Random Point in Non-overlapping Rectangles	Unavailable public link	Code	18/03/2023

Comments

Authors: farmerboy95